AI Insights for Human Intelligence

The comparison between artificial intelligence (AI) and human intelligence has been a heated debate ever since Turing envisioned thinking machines. Today AI is still not intelligent, nevertheless, we can draw lessons from it for our own intelligence.

• Is it possible for machines to think like humans?
• How far are we from intelligent machines taking the world?
• Is the artificial neural network inspired by the brain?

In all these questions and others, the focus is on shaping the future of AI. But why don’t we think about improving human intelligence by looking into AI? I can feel your suspicion, don’t worry and bear with me, this is not a post about genome editing to upgrade the brain.

Human intelligence is not just about the brain, education is an essential part of our intelligence too and we can improve human intelligence with a better education. But it seems like we are much more successful in training machines than we are in training humans.

There might be many possible explanations for this. AI is a mathematical construct and most of the time we can craft a performance metric to define better whereas education has economic, social, political, and religious components and the definition of better becomes subjective. In addition, in AI, we can experiment much more freely to find out which learning method works best. On the other hand, there are many limitations (finances, time, etc.) to experimentation in the field of education. Finally, there are benchmark datasets that help people around to world compare their machine learning methods. Such a universal comparison is very hard to achieve for education.

These challenges don’t mean we are hopeless. Asimov once said, “The saddest aspect of life right now is that science gathers knowledge faster than society gathers wisdom.” For a change, let’s use our AI knowledge to improve human intelligence.

Rule-based vs. Self-learning approach

There are two approaches to AI; a rule-based system where you hard code all the rules for the algorithm to follow and a self-learning approach (i.e. machine learning) where you show the data to the algorithm and it learns the patterns, relationships, transformations itself. There is a unanimous agreement on the fact that machine learning outperforms rule-based algorithms for perceptual tasks. In other words, we prefer to show, we don’t tell.

Yet, this is not what we do when it comes to human education. We tell, dictate, impose the so-called truths, instead of showing the data for students to learn their own truths. This prevents students from internalizing the concepts. This might be enough for a limited set of problems such as repetitive tasks. To deal with novel problems, however, one needs to bend and mix ideas comfortably. This only happens by understanding the essence of the concepts not by memorizing them.

The students are not called upon to know, but to memorize the contents narrated by the teacher.

— Paulo Freire

As we do in machine learning, we should rely on humans learning for themselves, in other words, self-education. Schools should be there to create an environment that can stimulate self-education.

…self-education is, I firmly believe, the only kind of education there is. The only function of a school is to make self-education easier; failing that, it does nothing.

— Isaac Asimov

How to stimulate self-learning?

Even if we agree that self-learning is the way forward, how do we execute it? AI researchers have been putting tremendous effort to study machine learning and we have an extensive body of knowledge that we can look into.

For many machine learning tasks, we use an optimization algorithm called gradient descent. This is actually how the machine learns. Understanding its basics is very easy. It is an iterative algorithm; it approaches the solution step by step. It starts by making a prediction, we give it feedback about how far it is from the truth and it makes a new slightly improved prediction. This sequence goes on and on until we are satisfied with the difference between the predictions and the truth. In other words, learning is an active step-by-step process where the algorithm rethinks its assumptions at every step and it improves a bit more.

I cannot think for others or without others, nor can others think for me. Even if the people's thinking is superstitious or naive, it is only as they rethink their assumptions in action that they can change. Producing and acting upon their own ideas -not consuming those of others- must constitute that process. - Paulo Freire

As you can see, gradient descent could help us understand how to execute self-learning. We can also learn some lessons by looking into the testing phase.

Everyone working on ML knows by heart that you train the algorithm with one dataset (called training data), and use a different dataset for testing (called test data) in order to make sure that the algorithm is not memorizing (overfitting) but actually learning. Of course, the training data and the test data must be from the same distribution. You cannot teach math and expect good answers to history questions.

If you are creating a cat classifier, for example, you train the algorithm by showing the pictures of the cats Garfield, Hello Kitty, Tigger… and test the algorithm with different cats: Felix, Cosmo, Figaro… If the algorithm can say that Felix is a cat, it has learned what catness really is. If the algorithm says that Garfield is a cat, it might have learned what catness is but it is also possible that it just memorized the fact Garfield = Cat. Therefore, every practitioner in this field agrees that we shouldn’t use training data for testing. Do you think this the case for human learning?

When it comes to educating our children, more often than not, we train and test them with a specific set of questions. However, the questions in life don’t have predefined, rigid structures. They constantly evolve. One can only handle them by internalizing concepts not memorizing them. Therefore we should challenge students with open-ended questions, confront them with uncertainty, let them speculate and explore the landscape themselves.

Optional example: How to teach derivatives?

To make things concrete, let’s compare rule-based approach and self-learning approach for teaching derivatives. Feel free to skip this part. The aim here is to show you how to stimulate self-learning for derivatives, it is not teaching derivatives.

Traditionally, derivatives are taught by introducing the derivative formula and showing the derivative of several common functions. Then, students memorize the formulas by solving some questions. This is just like the rule-based approach to AI where you hard code the rules that the algorithm should follow.

The traditional way to teach derivatives. Just like a rule-based approach to AI where you hard code the rules that the algorithm should follow.

Let’s look at an alternative approach, namely the self-learning approach. Like we do in machine learning, the aim here will be to create an environment that will stimulate self-learning. We will not dictate anything, students will learn themselves.

Change at an instant is the essence of derivatives, but change occurs over time whereas an instant is just one moment. People should feel this contradiction themselves in order to capture the idea of derivative. How can we achieve this?

You can open the floor to discussion with one of the Zeno’s paradoxes: “Suppose you wish to reach a wall 1 meter away from you. In order the achieve this, you first need to travel half the way and reach the middle (1/2 m). The same is true for the remaining distance. To travel the remaining 1/2 m you first need to reach the middle point (1/4 m). This goes on and on, and there will always an infinitesimal distance remaining between you and the wall. You can approach the wall but you can never reach it — or maybe you can reach the wall at infinity. In real life we know that we can actually reach the wall let’s discuss what is happening here…”

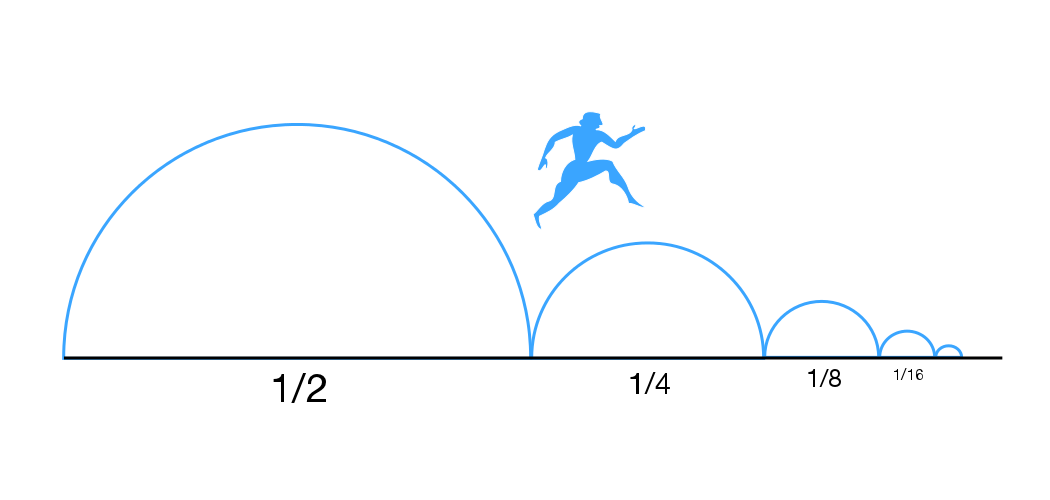One of Zeno's famous paradoxes

Hopefully, this discussion will lead them to grasp the concepts of infinitesimal and infinity or at least initiate a feel for them. If not, you iterate until they do, just like we do in gradient descent. Equipped with this understanding we can ask the students to talk about instantaneous velocity:

“Average velocity is the displacement over a specific time interval. But how do you measure instantaneous velocity? Instantaneous means the time interval is zero and you cannot move if the time doesn’t flow. It seems instantaneous velocity should be 0/0=undefined. What do you think about this?”

Again, after some iterations (5 epochs should be enough:), they will probably reach the conclusion that as the time interval approaches zero, average velocity approaches to the instantaneous velocity, just like we approach the wall in Zeno’s paradox. This is actually what derivative is (derivative of displacement as a function of time is velocity) and they reached this point themselves while trying to find answers to some questions. We can even reach the above equation from this understanding. I am not suggesting to omit the equations from education but students should understand the motivation behind those equations.

I am not an expert on teaching derivatives to humans therefore I tried to give a crude outline for self-learning approach for derivatives. What is important here is the approach, not derivatives. You can apply this concept to any subject. To teach photography, for example, instead of providing rules for a good photograph, you should direct students to good websites, books etc. for them to see and form their own understanding of photography. Meanwhile, you can organize exhibitions for them to share their photos and improve iteratively with constructive discussions.

If you are interested in learning the derivatives, watch this video by Grant Sanderson. It is a prime example of proper teaching. At some point, he asks some questions and says “pause and reflect”. This is the whole point, one needs pause and reflect in order to actually learn something.

He also says, “If that feels strange and paradoxical, good! You’re grappling with the same conflict that the fathers of calculus did…” In a sense, he is helping you to become Newton and this is what self-learning is.

Conclusions

It is possible to say that artificial intelligence is the simulation of human intelligence. It would be a huge waste if we don’t make use of its results:

• We should promote self-learning instead of rule-based learning. We know that machine learning is the way forward in the AI domain.
• Students should improve their assumptions themselves. Like we do in gradient descent, we might just supervise the learning process, giving students feedback at each step but not the solution.
• To make sure students are learning not memorizing, we should confront them with never seen before situations. In machine learning, we always test the algorithm with a dataset it has never seen before.

You might be thinking that these insights on education are already known and the correspondence between human intelligence and artificial intelligence is not that useful after all. But think about it again, the key here is that there is almost a full agreement on these insights in the AI domain, do you think the same is true for the human intelligence domain? I do realize that humans and machines are different and it is not possible to say that the correspondence is 100%. However, it is evident that there is a strong relationship. Let’s utilize this valuable similarity between human and machine learning to understand and overcome challenges in the way we educate our children.